数据结构与算法 -- 红黑树

11 Apr 2018

最近学新东西和写博客越来越不勤了。不管再忙，磨刀也不误砍柴工。人要不断的学习才能进步。继续从简单的开始吧。

前几个月了解了下红黑树相关的知识。发现红黑树还是很强大的。当然红黑树的学习难度也是比较大的，当时看了很多资料看起来都头晕。最后找到一篇“查找（一）史上最简单清晰的红黑树讲解”。发现博主确实不是吹牛，讲的十分通俗易懂。我再讲也不能比他要讲的好，所以就不再献丑了。这里仅对博主的文章作一些总结。文中所有其博文的原文均以引用来表示，图片也均来自于原博文。。

二叉查找树

对于有序的数组，我们可以使用二分查找大大的降低每次查找所需要的时间。但数据表不是一成不变的，现代很多应用都还需要很方便的对数据表进行插入，删除等操作。对于这些操作，数组实在很难应对。因此，我们引入链表，并将其与将二分查找结合起来，产生出了二叉查找树。

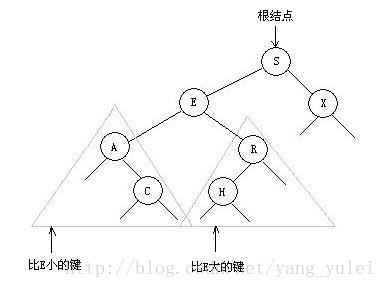
一颗二叉查找树（BST）是一颗二叉树，其中每个节点都含有一个可比较的键（以及相关联的值）且每个结点的键都大于其左子树中的任意结点的键而小于右子树的任意结点的键。如下图所示，数的深度就是从最上面的节点到最下面节点的节点数。

对于树的查找操作，如果树是空的，则查找未命中。如果被查找的键和根结点的键相等，查找命中。否则我们就在适当的子树中继续查找。如果被查找的键较小就选择左子树，较大就选择右子树。容易想像，平均所需查找时间与树的深度息息相关。树越深，平均所需查找时间就越长。而树的深度也与树的不平衡程度有关，根节点是最大的数的树显然是要比根节点是中位数的树要深很多。

平衡查找树，平衡二叉树，2-3查找树

为了定义一个树的平衡程度，我们引入平衡因子的概念：

二叉树上结点的平衡因子BF(BalanceFactor)定义为该结点的左子树深度减去它的右子树深度的绝对值。

显然，对于一个树节点来说，如果其平衡因子是其所允许的最小值,那么这个节点就是平衡的。而为了使查找树的深度最小，这就要求对于树的每个节点，它的平衡因子不能超过1，这样的树就被称为平衡查找树。而一个二叉树时时刻刻满足平衡查找树的条件，那这个树就被称为平衡二叉树(AVL树)，平衡二叉树的平衡因子不超过1。

可以看出，AVL树定义非常简单。但实际上在AVL树插入删除等操作中，为了一直满足左右子树深度之差不能超过一，我们需要做出很多判断以及操作(有兴趣可以看下AVL树是如何做的)。这使得AVL树虽然查找非常快，但插入和删除开销却较大。为了改进这部分开销，人们开发出另一种平衡查找树：2-3查找树(以下基本援引参考文章的内容)。

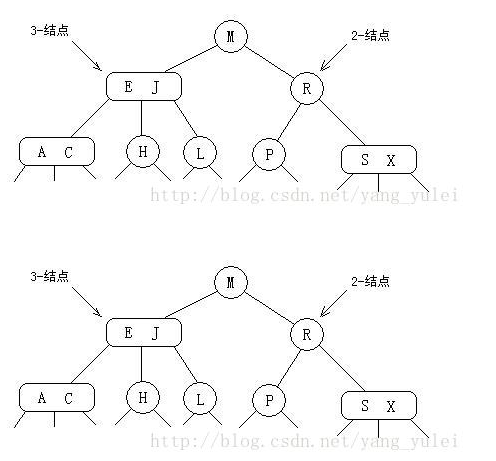
2-3查找树有两种节点: 2-结点：含有一个键(及值)和两条链接，左链接指向的2-3树中的键都小于该结点，右链接指向的2-3树中的键都大于该结点。
3-结点：含有两个键(及值)和三条链接，左链接指向的2-3树中的键都小于该结点，中链接指向的2-3树中的键都位于该结点的两个键之间，右链接指向的2-3树中的键都大于该结点
一颗完美平衡的2-3查找树中的所有节点的平衡因子为0。

对于2-3树的插入，规则如下:

对于2节点，将其变为3节点并将插入的数据保存即可
对于3节点，则先构造一个临时的4节点，然后将其分解为类似 “$\bigwedge$” 的符号并将这组节点插入。

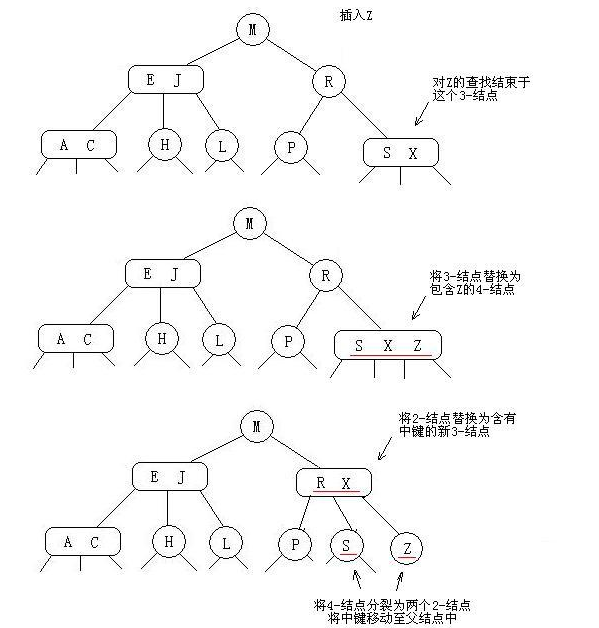从上面可以看出，对2-3树的插入如果不影响到到根节点，树的深度不会变化。而每次插入后，树仍然是完美平衡的。

红黑树

红黑树其实就是2-3树的二叉树形式。

对于2-3树，我们将3节点表示为一条左斜的红色链接相连的两个2-节点。这样，一个2-3树就转化为二叉树。这个转化而来的二叉树既是红黑树。

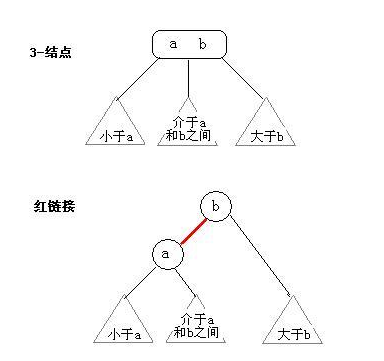
将2-3树转化为红黑树的一个优点就是我们不需要完全的维护两种不同的节点，只需要在标准二叉树中加入一些额外信息即可。当我们想要理解红黑树的插入，画法规则时，只需要将其在脑海中转化为2-3树。

红黑树的颜色表示

因为每个结点都只会有一条指向自己的链接（从它的父结点指向它），我们将链接的颜色保存在表示结点的Node数据类型的布尔变量color中（若指向它的链接是红色的，那么该变量为true，黑色则为false）。
当我们提到一个结点颜色时，我们指的是指向该结点的链接的颜色。

红黑树的性质

当我们了解红黑树的实质后，它的性质也就不难理解。

红黑树是满足下列条件的二叉查找树：
1.红链接均为左链接。
2.没有任何一个结点同时和两条红链接相连。
3.该树是完美黑色平衡的，即任意空链接到根结点的路径上的黑链接数量相同。